はじめに
ユービーセキュアでWebエンジニアとしてもっさり開発に携わっている田中です。弊社はWebセキュリティの会社ですが、本記事では前の記事『Web Audio APIでシンセサイザーを作って遊ぶ(前編)』に続き、シンセサイザーの仕組みを解説していきます。
前編では、Web Audio APIの基本的な使い方を述べました。本記事 (中編) では実際にシンセサイザーの仕組みに入門します。前編の記事で説明したWeb Audio APIの使い方を利用しますのでわからなくなったら戻って読み直すのもよいでしょう。
え? 前後編じゃなかったのかって? 3倍返しだ!!!
この記事の目標
この記事ではシンセサイザーの基本的な要素の理解が目標です。音についての一般的な知識やシンセサイザーにおける音色の作り出し方などを知り、後編のシンセサイザーアプリケーションへの土台とします。
シンセサイザー入門
記事のメイントピックとなるシンセサイザーのしくみを述べていきますが、各個の節では新しい概念の導入とその実装が入り乱れて長くなることが予想されるのでここに概要を示しておきます。
まず、音の種類と性質を述べたあとにドレミ…の音階と周波数を対応づけるコードを書き、音階とは何なのかを軽く解説します。
次に、音色の種類を増やします。前節では音色にサイン波を用いて説明しますが、実際それだけでは物足りませんよね。そのためほかの波形や音色の変化をつける手法について説明します。
音の3要素
シンセサイザーで音を合成するのですが、そもそも音って何でしょう。耳で捉える場合、音とは空気の振動です。つまり疎と密の波です。音を電気・電子機器で扱う場合には、時間方向に変化する電圧の強弱として表現されます。それらから一般化して、音は波として扱われます。
音楽の分野では、音は2種に大別されます。「楽音」と「噪音」です。楽音はメロディを構成するのに用いられる、高さの感じられる音のことです。楽音には「強さ」「高さ」「音色」の3つの要素があります。一方で噪音は打楽器のような音程の感じられない音のことです。
楽音の「強さ」は振動の強さ、つまり振動の揺れの大きさで、これが大きいほど音も大きく感じられます。楽音の「高さ」は振動の周期が対応し、これが大きいほど音が高く感じられます。楽音の「音色」は振動が繰り返す波形のパターンで、これが時間経過で変化することで様々な音色に感じられます。
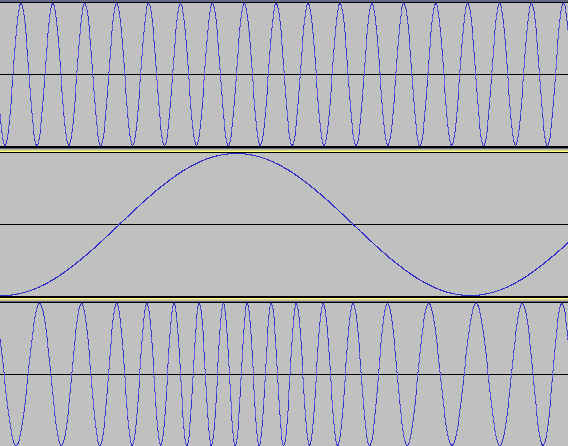
楽音は周期的な波であり、周期を構成する波の繰り返しの頻度 (周波数; 単位はHz) が音の高さとして感じられます。以下に440Hzのサイン波と880Hzのサイン波の波形を示します。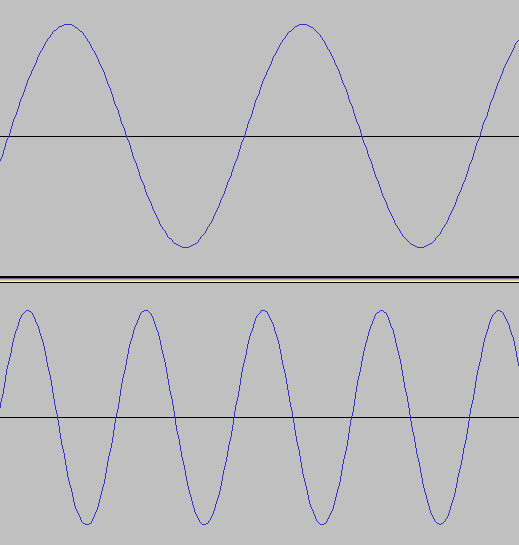
上が440Hzの波形、下が880Hzの波形です。同じ形が繰り返し現われているのがわかると思います。音名でいうとどちらの波形もラの音です。周波数が大きいほうが高く感じられ、周波数が2倍になると1オクターブ高い音になります。
音名と周波数の対応づけ
前の節で「音名」「ラ」などの言葉が出てきましたが、オシレータから音を鳴らすにはその音の周波数を知らなければなりません。音楽の授業でもなんとなく「ドレミファソラシド」を習いますがそれら音名と周波数との対応はどうなっているのでしょう。
音名とは音階上の各音につけられた名前のことで、じゃあ音階はというと、降順あるいは昇順で「これと決めておいた音」を並べたものです。しかもどれも西洋音楽での用語です。ややこしいですね。「ドの音」とか「ソのシャープ」とかいう名前が指すものは何なのか、どうやって決めるのか。それを規定するのが音律です。
音律は、五線譜上のどの位置がどの周波数であるかを決めるもの、というとざっくりですが理解しやすいと思います。前節で「2つの音が1オクターブ離れると周波数が2倍になる」と述べました。この事実といくつかの仮定を置くと (音律; 音の間の関係)、基準となる周波数 (たとえば440Hz) を元にして同じ (響きの) 音にもどってくる周波数の配列 (つまり音階) を確定することができます。音律があって、音名や音階がある、ということになります。
なぜこんな まわりくどい めんどくさい 説明をしたかというと、音律は一つではないからです。そこにはさまざまな歴史がありいろいろと事情もあるのですがそのあたりは講談社より出版されている『音律と音階の科学 新装版 ドレミ…はどのように生まれたか』を読んでみてください。おもしろいです。
ともかく、ここでは現代の大抵の音楽で採用されている十二平均律を採用して音階を決定します。十二平均律は「1オクターブ離れた2音の周波数をちょうど均等に割る (平均)」とピアノの鍵盤の白黒合わせて12音が出てくる、という音律です。発明されたのはバッハの晩年のころで、これにより曲の雰囲気を途中でガラッと変える「転調」「移調」といった技法が使えるようになるのです。欠点として、各音を重ねて和音をつくるときにわずかにうなりが発生するなどがあり (ピタゴラスのコンマ)、完全な響きが得られないようです。
ともあれ、十二平均律を採用するとプログラムでの周波数計算はとても楽になります。音階を1段ずつ上がっていくとき周波数は同じ比率で上がっていきます (等比数列)。この記事では以下の事実や前提に立って音階と周波数を対応づけます:
- 周波数が
nである音の1オクターブ上の音の周波数は2 * nである - 十二平均律を採用する
-
- 1オクターブを隣り合う音の比率が
低い音 : 高い音 = 1: 2^(1/12)となるように分割する - つまり、たとえばドの周波数を
2^(1/12)倍するとド#になり、それを12回繰り返すと1オクターブ上のドになる
- 1オクターブを隣り合う音の比率が
- 全ての音に数字を割り振り、それをプログラム上で扱う。440Hzの音を69とする。
-
- 鍵盤上の位置と考えるとわかりやすい
- 参考: MIDIノートナンバーの記事を参照
-
// 基準となるラの音 (concert A) の周波数
const concert_a_freq = 440;
// 基準となるラの音 (concert A) のMIDIノートナンバー
const concert_a_notenum = 69;
// MIDIノートナンバーを十二平均律で周波数に変換する関数
const convert_to_frequency = (notenum) => {
// 基準音から何音高い/低いかを計算する
const from_concert_a = notenum - concert_a_notenum;
// 周波数を実際に計算する
// 十二平均律では2音の最小の周波数差は`2^(1/12)`となる
const freq = Math.pow(2, from_concert_a / 12) * concert_a_freq;
return freq;
};
// 音を慣らす準備準備
ctx = new AudioContext()
osc = new OscillatorNode(ctx)
// 基準音 (ラ: 440Hz, 69番) を設定
osc.frequency.value = convert_to_frequency(69)
// オシレータの処理を開始
osc.connect(ctx.destination)
osc.start()
// オシレータの周波数を変更
// 基準音より低くて一番近いド (60番) に設定
osc.frequency.value = convert_to_frequency(60)
音色を増やす
現在鳴らすことができるのは時報の音のサイン波だけですが、サイン波の音は「純音」ともいい、そのままではなんとも味気ない感じがします。この節では鳴らせる音色を増やしていくことにしましょう。音色を変えるということは波形を変えるということですが、さまざまな波形の変え方からここでは3つを選んで解説します。
違う波形を選ぶ
まず一番簡単なのは、オシレータが発する1周期分の波形を変えてしまうことです。Web Audio APIのOscillatorNodeにtypeというプロパティがありました。これを変えることで、オシレータの一周期分の波形の形を変えることが可能です。たとえばosc.type = "square"としてみると「矩形波」という種類の音がでます。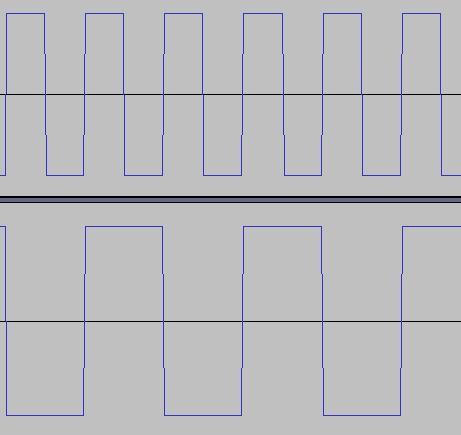
矩形波は波形が文字通り四角形 (矩形) になるためそう呼ばれています。レトロなゲーム機でよく聞いていたなじみのある音だと思います。この矩形波は最大値と最小値を交互に繰り返す波形で、最大値のときの時間と最小値のときの時間が同じです。この最大値と最小値の時間の比を「デューティ比」と言い、これを変化させるとまた音色が変わります。OscillatorNodeではデューティ比を変化させた音は出せないようなのですが、レトロなゲーム機ではこのデューティ比をパラメータとして設定できるためよく用いられており、その音に聞きおぼえがあるかもしれません。
また、osc.type = sawtoothとするとブー、というブザーのような音がします。
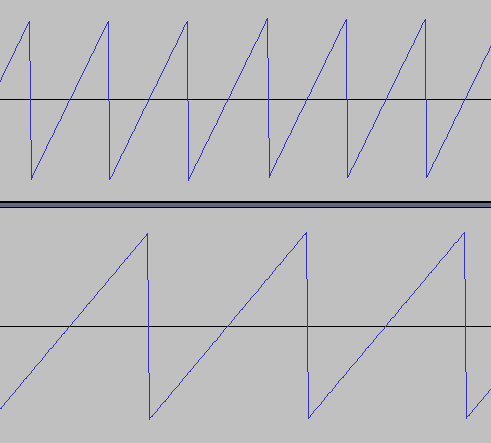
こちらはノコギリ波といい、矩形波とともにシンセサイザーの基本波形としてよく登場します。ノコギリ波は矩形波よりも豊かな倍音を持つため、筆者はしばしばノコギリ波から音づくりを開始します。
波形を変形させる
この節と次の節の内容は後編で作成するプログラムでは簡単化のため扱いませんが、シンセサイザーでの音作りにとって重要です。
1周期分の波形を変えるだけでも音が変わりますが、これでは複雑な波形をつくりだすのにいちいち波形のデータを用意せねばならないだけでなく、1周期を超える変化を音に盛り込むことができません。そこでここでは2つの波形を元にして新たな波形をつくりだす「変調」という方法を用いて音色を作ります。
変調には2つのオシレータを用います。1つめのオシレータの波形を、2つめのオシレータの波形の力で変形させるのが変調です。このとき2つめのオシレータのことをモジュレータ (modulator) といいます。具体例を見ましょう。下記の図は2つのサイン波を用いて振幅変調 (AM; Amplifier Modulation)を行った図です。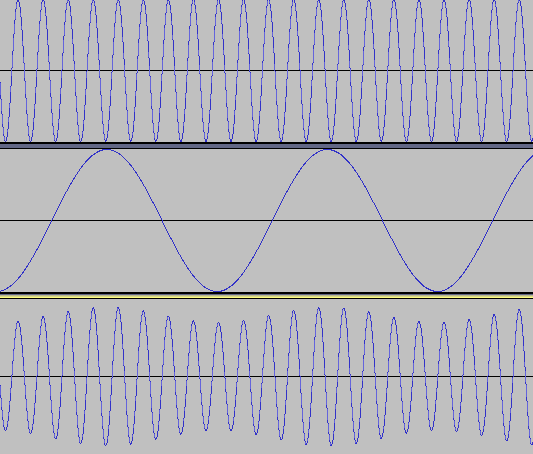
図の上2つの波形(オシレータ)を用意し、1つめの波形の振幅(つまり音の大きさ)を2つめの波形で揺らして(変調)います。プログラムでいうとちょうど以下のようなコードが対応するでしょう:
let ctx = new AudioContext()
// メインの (揺らされる)オシレータ
let osc1 = new OscillatorNode(ctx)
osc1.frequency.value = 440
// 揺らすほうのオシレータ (モジュレータ)
let osc2 = new OscillatorNode(ctx)
osc2.frequency.value = 4
// 音量を上げる (かけ算をする) ノード
let gain = new GainNode(ctx) // モジュレーションに利用
let gain2 = new GainNode(ctx) // モジュレーションの適用量を調整するのに利用
gain2.gain.value = 0.3
// osc1の音量(ゲイン)を操作できるようGainNodeに接続
osc1.connect(gain)
// osc2はゲインを変化させるので、GainNodeのgainパラメータに接続
osc2.connect(gain.gain)
gain.connect(gain2)
// GainNodeをスピーカーに接続して音をスタート
gain2.connect(ctx.destination)
osc1.start()
// 変調を開始
osc2.start()
osc2.frequency.valueが音量の上下の周期に、gain2.gain.valueが音量の上下の強さに対応しています。変調の方式には他に周波数変調 (FM; Frequency Modulation)というのもあります。これは揺らす方のオシレータの出力を別のオシレータの周波数に接続してオシレータの波形の周波数自体を揺らす方式です。
図の上2つの波形がそれぞれ440Hzの波形と80Hzのモジュレータの波形です。3つめの波形の周波数(つまり音の高さ)が、モジュレータの動きに合わせて高く(密)なったり低く(疎)なったりを繰り返しているのがわかると思います。モジュレータの周波数が低いうちはビブラートのような音ができますが、周波数を上げていくと徐々に金属的な音になっていきます。以下に周波数変調を行うコードを用意してみたので、
osc2.frequency.valueやgain.gain.valueを開発者コンソールで変更し音の変換を体験してみてください。let ctx = new AudioContext()
// メインの (揺らされる)オシレータ
let osc1 = new OscillatorNode(ctx)
osc1.frequency.value = 440
// 揺らすほうのオシレータ (モジュレータ)
let osc2 = new OscillatorNode(ctx)
osc2.frequency.value = 5
// モジュレーションに利用
let gain = new GainNode(ctx)
gain.gain.value = 5
// osc2はゲインを変化させるので、osc1のfrequencyパラメータに接続
osc2.connect(gain)
gain.connect(osc1.frequency)
// GainNodeをスピーカーに接続して音をスタート
osc1.connect(ctx.destination)
osc1.start()
// 変調を開始
osc2.start()
高い音だけをカットする
この節の内容も後編で作成するプログラムでは簡単化のため扱いませんが、シンセサイザーでの音作りにおいては基本中の基本です。
ふだんよく聞く音 (楽器の音、水の音、キーボードの打鍵音、etc.) は、実はさまざまな周波数の純音が音量を変化させながら同時に鳴っているという点で純音と異なります。逆に言えばあらゆる音は純音つまりサイン波を同時に演奏したものだと考えることができるのです。ということは「ある音はその瞬間どの周波数がどれだけの音量で鳴っているか」という周波数の分布を考えることができます。これをスペクトラムといい、信号から周波数の分布を計算してくれる機械をスペクトラム・アナライザーといいます。むずかしい話に聞こえますがこんな図を出せばピンとくるのではないでしょうか (Windows Media Playerのスクリーンショットです)。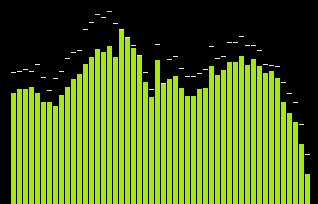
音楽プレーヤーにはよくビジュアライザとしてスペクトラム・アナライザーが搭載されているので見たことがあるでしょう。見方を説明します。横軸が周波数で左が低い音、右が高い音です。縦軸は音量を表しており、棒が高いほどその周波数の純音が大きいことを表します。したがってたとえば次のようなスペクトラム (こちらはオープンソースのオーディオ編集・解析ソフトウェアのAudacityのものです)を見ると、
左側が高くて右に行くほど低くなっているので「この音はきっと低い音が強くて、あまり高音は鳴っていないんだな」ということがわかります。使った音声ファイルはWikimediaにあるこちらですのでスペクトラムと合わせて聞いてみてみてください。
さて、シンセサイザーの話に戻ります。
シンセサイザーのオシレータは基本的な音しか出せないと前節で述べました。これを複雑にする2つめの方法は、この周波数分布を多少いじってやる、という方法です。イコライザーやフィルターといったエフェクトを適用することで実現しますが、ここではフィルターの例を述べます。
フィルター (filter) とは、特定の周波数帯のみを通す (あるいは通さない) という処理をするエフェクトです。いちばん基本的なフィルターの1つとしてローパスフィルター (low-pass filter) やハイパスフィルター (high-pass filter) があります。これらはある周波数を境目として (カットオフ周波数といいます)、周波数分布の中の片側の音をカットするエフェクトです。周波数の低いほうを残すのか高いほうを残すのかで、ローパス・ハイパスと分かれているというわけです。
ここで、440Hzのノコギリ波のスペクトラムを見てみましょう。
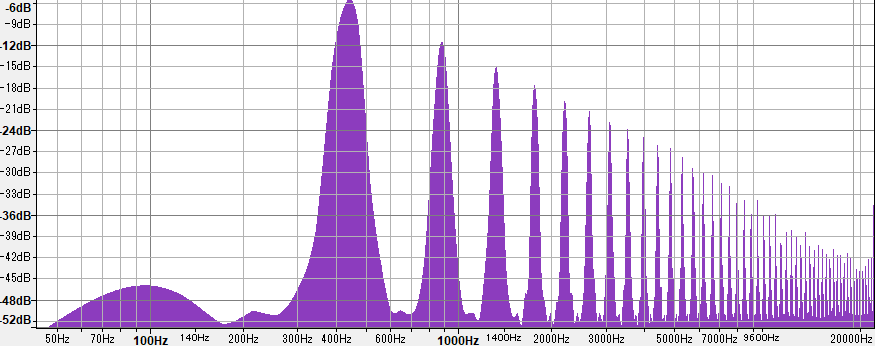
440Hzあたりに1番高い山があり、すぐ右にある次の山は2番目に高く、…といった感じで続いています。1番高い山によってわれわれはこの音を440Hzの音だと感じるのですが、この音を基音といいます。以降に続く音は基音の整数倍の周波数を持ち、倍音と呼ばれています。倍音があることで、また時間とともに音量が変わっていくことで、さまざまな音色が感じられるのです。
次に、440Hzのノコギリ波をローパスフィルター (カットオフ周波数1200Hz、減衰傾度24dB) に通したスペクトラムを見てみましょう。
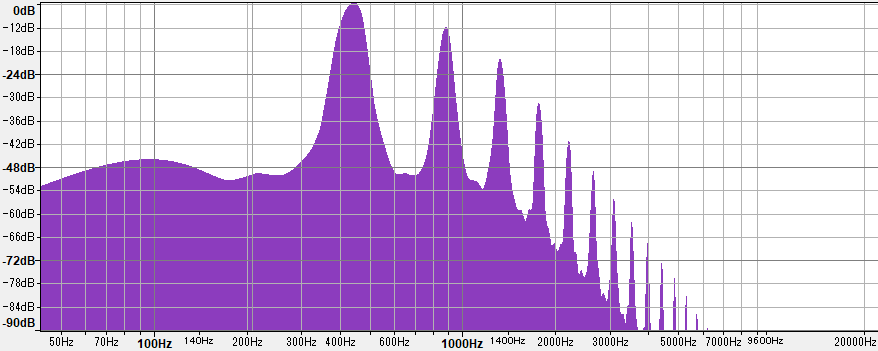
図の左にある一番高いところの音量の値に注意しましょう。図の高さは同じですが最大音量がフィルターの適用前後で違います。ここでは音量は0を最大としてdB (デシベル) で表現されています。dBという単位は対数ですから、負の値ということは小さくなるほど大きい (0に近づく) ということになります。フィルター適用前が-6dBで適用後が0dBですから、フィルターの適用によって基音の音量は2の6乗倍つまり64倍になっています。そして1200Hzを境にして倍音が小さくなっているため、この音を聞くとくぐもった (高音域が削られた) ように聞こえます。
フィルターの適用前後で基音の音量が増えているのはフィルターの特性によるものです。フィルターはカットオフ周波数を境目に音をカットすると述べましたが、すっぱりとカットできるわけではありません。カットオフ周波数以降の音の減衰のしかたのイメージを以下に、AudacityのFilter Curve EQを用いて図としました。
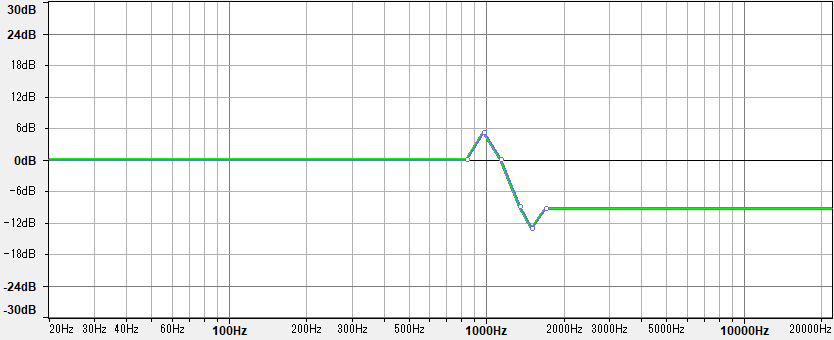
フィルターによる高音域・低音域の除去は、減衰を急にするとカットオフ周波数周辺の音の音量が逆に上がってしまうのです。そのため減衰傾度を高くするとカットオフ周波数周辺の音が強調され、音が変わってしまいます。シンセサイザーではローパスまたはハイパスフィルターのこれらの性質を利用して、音をくもらせたり特定の周波数を強調したりすることで音づくりをしていきます。
ここまでで述べたことをWeb Audio APIのBiquadFilterNodeを用いて試してみましょう。
let ctx = new AudioContext()
// メインのオシレータ
let osc = new OscillatorNode(ctx)
osc.type = "sawtooth"
osc.frequency.value = 110
// フィルターのカットオフ周波数のモジュレータ
let mod = new OscillatorNode(ctx)
mod.frequency.value = 2
// モジュレーションの適用量
let gain = new GainNode(ctx)
gain.gain.value = 200
// フィルターのカットオフ周波数 (定数)
let freq = new ConstantSourceNode(ctx)
freq.offset.value = 440
// ローパスフィルター
let lpf = new BiquadFilterNode(ctx)
lpf.type = "lowpass"
lpf.frequency.value = 0
lpf.Q = 20
// モジュレータと定数値をフィルタのカットオフ周波数として入力
mod.connect(gain)
freq.connect(lpf.frequency)
gain.connect(lpf.frequency)
// フィルターにosc1を接続
osc.connect(lpf)
// BiquadFilterNodeをスピーカーに接続して音をスタート
lpf.connect(ctx.destination)
osc.start()
// 変調を開始
freq.start()
mod.start()
freq.offset.valueを変更することでカットオフ周波数を変更できます。gain.gain.valueはカットオフ周波数にモジュレーション用に入力されているサイン波の強さを決定します。lpf.Qはカットオフの減衰傾度で、これを高くすると急峻なカットオフが行われ、カットオフ周波数周辺の音の増加も大きくなります。
おわりに
本記事ではシンセサイザーの基本的なしくみに、Web Audio APIで実験をしながら入門しました。後編ではこれまでの総括として、ブラウザで動く音楽演奏プログラムを作成します。ご期待ください。














